’Ontdekken’ en ‘ontdekken’ is twee…

Geachte heer Schmeier,

Pas op 9 november 2020 zag ik op het internet deze foto bij uw artikel ‘Leren rekenen of ontdekkend kangoeroes leren tellen’ (Opinie, internetversie van NRC-Handelsblad, 6 februari 2019):

Bij het onderwerp ‘ontdekkend leren’ ben ik nauw betrokken. Mijn bedrijf heet ‘Ontdekkend Leren’ en ik ben de maker van de leeslijn ‘Ontdekkend Leren Lezen’ (OLL). Ik vind dit een misleidende foto in verband met ‘ontdekkend leren’ (in dit geval van tellen).
Als de foto niet door u is voorgesteld, zou ik willen weten of u er een onschuldige vorm van ironie in ziet en, als u zich kunt voorstellen dat ik er vanuit Ontdekkend Leren iets belachelijks in zie, u in het tweede geval bij de redactie protest wilt aantekenen.

‘Ontdekkend kangoeroes leren tellen’?
Wat Ontdekkend Leren betreft, weliswaar komt er vroeg of laat ook een ‘Ontdekkend Leren Rekenen’ (OLR), maar dat is er nu nog niet. Die foto geeft zonder meer een caricaturaal beeld van ‘Ontdekkend Leren’ in het algemeen en ook van het toekomstige OLR in het bijzonder.
Op cursussen en lezingen vertel ik soms wel eens iets over OLR en dan laat ik als voorbeeld van een ontdekblad het ontdekblad voor ‘7’ zien:

Dit ontdekblad volgt op dat van het ontdekblad voor ‘6’. Vandaar linksboven 6 aardbeien plus 1 aardbei. Het lijkt me voor elk weldenkend mens duidelijk dat dit heel wat anders is dan het wanordelijke ‘zoekplaatje’ van de foto in de krant.

Het begrip ‘ontdekken’ in de zin van ‘Ontdekkend Leren’
Het woord ‘ontdekkend’ in ‘Ontdekkend Leren’ en ‘Ontdekkend Leren Rekenen’ voldoet aan vier kenmerken – ze blijken ook op te te gaan voor ontdekken in de wetenschap:

Iemand beschikt over een bepaalde achtergrondkennis die hij op goede gronden houdbaar acht – in het ontdekblad: kennis van het getal ‘6’; in de wetenschap: ‘iedereen ziet rood als rood’.
Ten opzichte van die achtergrondkennis neemt diegene iets waar, dat vanuit die achtergrondkennis niet te begrijpen is – in het ontdekblad: het getal ‘7’; in de wetenschap: ‘iemand ziet een rood zegel dat op groen gras is gevallen, niet’.
Diegene probeert dat nieuwe te begrijpen – in het ontdekblad: ‘zes plus een is zeven, wat als “7” wordt genoteerd’; in de wetenschap: ‘er bestaat zoiets als kleurenblindheid’.
Diegene toetst zijn vermoeden van kenmerk 3 – in het ontdekblad telt het kind niet alleen de aardbeien, maar ook de ezels en de molens; het blijkt dat 7=7, ongeacht de ruimtelijke ordening van de elementen (kleuters, die wel vooruit kunnen tellen maar niet rekenrijp zijn, denken namelijk dat * * * * * meer sterren bevat dan *****); in de wetenschap: ‘ik laat diegene allerlei verschillend gekleurde linten twee aan twee tegelijk zien om te kijken of diegene inderdaad rood en groen met elkaar verwisselt’, wat het geval bleek te zijn.

Ontdekkend Leren Lezen (OLL)
Deze vier kenmerken gaan ook op voor een ontdekking in OLL, dat sedert 13 november 2018 volledig beschikbaar is voor het onderwijs. Zie het ontdekblad bij de letter ‘k’:

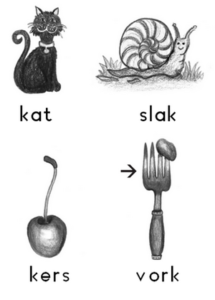
1. De achtergrondkennis is dat het kind de letters ‘a’, ‘t’, ‘s’, ‘l’, ‘e’, ‘r’, ‘v’ en ‘o’ al in eerdere hoofdstukken heeft ontdekt.
2. Het ‘figuurtje’ ‘k’ is in beginsel dus nieuw – behalve als het kind bijvoorbeeld Katja heet en haar naam kan schrijven.
3. Het kind herkent linksboven een poes en denkt dat er ‘poes’ onder staat, dus dat ‘k’ als /p/ klinkt.
4. Dit trekt het na, maar de woorden ‘pers’, ‘slap’ en ‘vorp’ passen niet bij de plaatjes.
3´. Het vermoedt dat linksonder een kers is afgebeeld en dat het woord dus ‘kers’ luidt.
4´. Het trekt ook dit vermoeden na. Inderdaad: ‘vork’ en ‘slak’ passen bij de plaatjes, net als ‘kat’ bij het plaatje linksboven.

Uw begrip ‘ontdekkend leren’
Ik zit dus zelf met een onbegrepen verschijnsel (kenmerk 2): u gebruikt de term ‘ontdekkend leren’ in een heel andere betekenis dan ik.
   Pas op 19 november 2020 kreeg ik toegang tot uw artikel en heb ik het kunnen lezen. Ik kreeg het vermoeden dat u ‘realistisch rekenen’ ‘ontdekkend’ noemt. U schrijft bijvoorbeeld: ‘Realistische rekenmethodes leggen bewust de leerstof niet uit, omdat kinderen het zelf moeten ontdekken’ (mijn cursiveringen).
   Meteen na uw artikel heb ik Funnekotters artikel van 1 februari 2019, waar u naar verwijst, gelezen. Deze haalt u aan: ‘Directe instructie door de docent […] is effectiever dan het zelfstandig, ontdekkend leren van het realistisch rekenen’ en ‘Ontdekkend, realistisch rekenen heeft slechts een effectgrootte van 0.11’ (mijn cursiveringen).
   U bent de enige die hier helderheid in kan brengen: is mijn vermoeden houdbaar of niet?
   Of uw antwoord ja of nee is, graag een toelichting. Ook vraag ik u of realistisch rekenen volgens u ‘ontdekkend’ is in de zin van de vier kenmerken? Zo ja, dan zou ik graag enkele aanhalingen van de aanhangers van realistisch rekenen zien, waaruit blijkt dat zij realistisch rekenen ook ‘ontdekkend’ noemen en, zo ja, waarom.
   Volgens mij is ‘ontdekkend’ van ‘realistisch rekenen’ wat anders dan ‘ontdekkend’ van OLR en OLS. ‘Ontdekkend’ en ‘ontdekkend’ is kennelijk twee… Vooralsnog word ik hierin bevestigd door wat ik bij Freudenthal, de geestelijke vader van realistisch rekenen, over ‘ontdekkend leren’ lees: ‘Ontdekkend leren; dat wil zeggen ont-dekken wat door iemand anders was be-dekt – verborgen paaseieren’ (Revisiting mathematical education, p.46). Ook een caricatuur, die niets met die vier kenmerken te maken heeft.

Nog vier puntjes
1. Als Funnekotter u in het geval van de effectgrootte van 0.11 juist heeft aangehaald, wilt u me dan laten weten wat er met die 0.11 aan de hand is? In Hatties top-138 (2009, p.297-300) staat namelijk maar één invloed met een effectgrootte van 0.11: ‘trainen van de leerkracht’ (op plaats 124). Valt voor u ‘realistisch rekenen’ inderdaad onder ‘trainen van de leerkracht’?
2. De invloed ‘directe instructie’ heeft inderdaad een effectgrootte van 0.59 (op plaats 26). OLR en OLL zijn op de psychologische ontwikkeling van het kind gebaseerd en vallen dus onder ‘ontwikkelingsprogramma’s’ (‘Piagetian programs’). Hun effectgrootte is 1.28 (op plaats 2) – meer dan twee keer zo groot als 0.59 voor directie instructie. Graag uw reactie hierop.
3. Op p.26 van uw boek over EDI (2020) schrijft u allerlei zaken die u aan ‘ontdekkend leren’ toedicht, maar in feite thuishoren bij ‘realistisch rekenen’ en bij andere onderwijsvormen in de geest van Vygotskij’s ‘zone van de naaste ontwikkeling’. Ik hoop dat u dat in een volgende druk zult aanpassen. Ik doel op wat u schrijft over de Commissie Dijsselbloem schrijft (zij zegt zelf niets over ontdekkend leren – dat doet vooral Van der Werf), over staatssecretaris Dekker (graag een tekst van hem waarin hij pleit voor ‘ontdekkend leren’), over Curriculum.nu en diens pleidooi voor ‘ontdekkend leren’.
4. Ik herken van OLR meer in wat u over ‘traditioneel rekenonderwijs’ schrijft, dan in wat u over ‘realistisch rekenen’ schrijft. In dat opzicht staan uw ‘expliciet directe instructie’ en mijn ‘ontdekkend leren’ dus dicht bij elkaar.

Ewald Vervaet, Amsterdam, 23 november 2020

—————————————————————————————

Laatste bewerking van deze webpagina: 23 november 2020